통계 데이터의 정확성은 아무리 철저한 절차와 효율적인 장비를 사용하더라도 항상 의문의 여지가 남습니다. 다행히도 엑셀은 이러한 불확실성을 측정하고 관리하는 데 매우 유용한 도구입니다. 특히 표본의 표준 편차를 기반으로 불확실성을 계산하는 데 탁월한 기능을 제공합니다.
엑셀에는 다양한 통계 공식을 활용하여 불확실성을 손쉽게 계산할 수 있습니다. 본 글에서는 산술 평균, 표준 편차, 표준 오차를 계산하는 방법을 살펴보고, 엑셀 차트에 이러한 불확실성을 시각적으로 표시하는 방법까지 자세히 알아보겠습니다.
아래의 샘플 데이터를 활용하여 함께 실습해 보겠습니다.

위 데이터는 5명의 사람이 측정한 값을 나타냅니다. 측정값들이 서로 다르기 때문에 실제 값에 대한 불확실성이 존재하게 됩니다.
측정값의 산술 평균 계산
다양한 값들이 모여 있을 때, 이들의 평균을 구하는 것은 합리적인 추정치를 얻는 좋은 방법입니다. 이 값은 산술 평균이라고도 불립니다.
엑셀에서는 AVERAGE 함수를 사용하여 산술 평균을 아주 쉽게 계산할 수 있습니다.
위 샘플 데이터에서 다음 공식을 사용하면 됩니다:
=AVERAGE(B2:B6)

측정값의 표준 편차 계산
표준 편차는 데이터가 평균값에서 얼마나 넓게 흩어져 있는지 보여주는 지표입니다. 즉, 데이터의 변동성을 나타냅니다.
엑셀에는 여러 가지 표준 편차 함수가 있습니다. 그중에서도 가장 많이 사용되는 함수는 STDEV.P와 STDEV.S입니다.
STDEV.P는 전체 모집단의 표준 편차를 계산하는 데 사용되며, STDEV.S는 모집단에서 추출한 표본의 표준 편차를 계산하는 데 사용됩니다.
위 예시에서는 데이터 세트의 5개 값을 모두 사용하므로 STDEV.P 함수를 사용합니다.
사용법은 AVERAGE 함수와 유사하며, 다음과 같은 공식을 적용할 수 있습니다.
=STDEV.P(B2:B6)

위 데이터 세트의 표준 편차는 0.16입니다. 이 숫자는 각 측정값이 평균값에서 평균적으로 얼마나 떨어져 있는지를 나타냅니다.
표준 오차 계산
표준 편차를 계산한 후에는 표준 오차를 구할 수 있습니다.
표준 오차는 표준 편차를 측정 횟수의 제곱근으로 나눈 값입니다. 이는 표본 평균이 모집단 평균과 얼마나 차이가 날 수 있는지를 보여주는 지표입니다.
아래 공식은 샘플 데이터의 표준 오차를 계산하는 데 사용됩니다.
=D5/SQRT(COUNT(B2:B6))

오차 막대를 사용하여 차트에 불확실성 표시
엑셀은 차트에 표준 편차 또는 불확실성 한계를 시각적으로 표시하는 기능을 제공합니다. 오차 막대를 추가하면 이를 쉽게 구현할 수 있습니다.
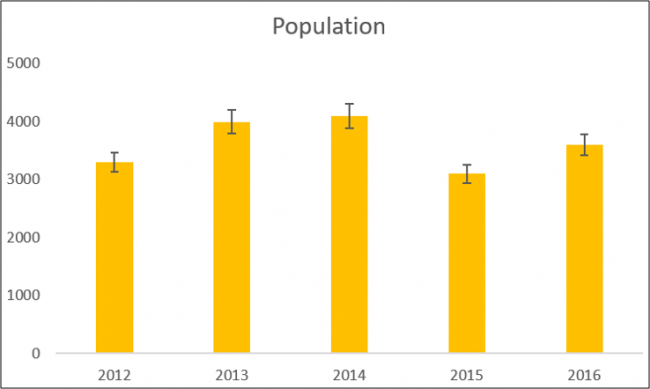
다음은 5년 동안의 인구 측정 데이터를 막대 그래프로 나타낸 예시입니다.

차트를 선택한 후 디자인 탭에서 “차트 요소 추가”를 클릭합니다.
나타나는 메뉴에서 오차 막대를 선택하고 원하는 유형을 선택합니다.

앞서 계산한 표준 오차나 표준 편차를 오차 막대로 표시할 수 있습니다. 또한 백분율 오류를 표시하는 옵션도 있으며, 기본값은 5%로 설정되어 있습니다.
위 예에서는 백분율을 표시하도록 설정했습니다.
오차 막대는 여러 가지 방식으로 사용자 정의할 수 있습니다.
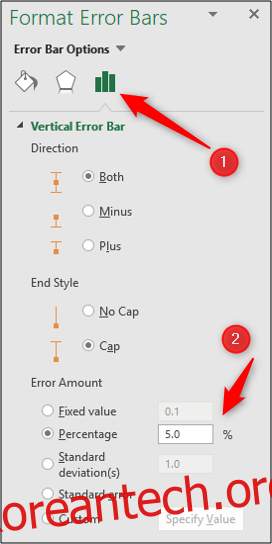
차트에서 오차 막대를 두 번 클릭하면 “오차 막대 서식” 창이 열립니다. 여기서 “오차 막대 옵션” 범주를 선택합니다.
이 창에서는 백분율, 표준 편차 값, 또는 통계 공식으로 계산한 사용자 지정 값을 선택하여 오차 막대를 상세하게 조정할 수 있습니다.
엑셀은 통계 분석과 보고에 매우 유용한 도구입니다. 다양한 불확실성 계산 기능을 통해 데이터 분석을 더욱 정확하고 신뢰성 있게 만들 수 있습니다.