파이썬에서 파스칼의 삼각형을 인쇄하는 방법

파이썬에서 파스칼의 삼각형 출력하기: 단계별 가이드

이 튜토리얼에서는 주어진 행 수에 따라 파이썬으로 파스칼의 삼각형을 생성하고 표시하는 여러 가지 접근 방식을 살펴보겠습니다. 파스칼의 삼각형이 무엇인지, 그리고 어떻게 구성되는지에 대한 기본 개념부터 시작하여, 파이썬 함수를 구현하고 성능을 최적화하는 단계를 알아볼 것입니다.

시작해볼까요?

파스칼의 삼각형이란 무엇이고 어떻게 생성하나요?

파스칼의 삼각형은 다양한 수학적 및 프로그래밍 문제에서 자주 등장하며, 주어진 행 수에 따라 이 삼각형을 출력하는 것은 코딩 면접에서 인기 있는 질문 중 하나입니다.

파스칼의 삼각형에서, n번째 행은 n개의 숫자로 구성됩니다. 첫 번째 행은 숫자 ‘1’ 하나로 시작하며, 다음 행의 각 숫자는 바로 위의 두 숫자의 합으로 계산됩니다.

다음 이미지는 5개의 행으로 구성된 파스칼의 삼각형의 구조를 시각적으로 보여줍니다.

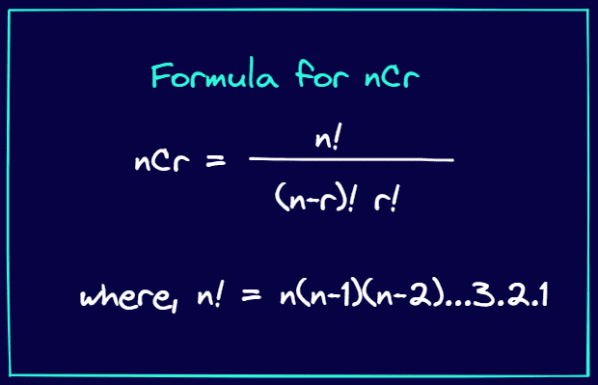
윗 숫자가 하나만 있는 경우, 계산 시 0을 고려해야 함을 기억하세요.

연습 삼아, 위에서 설명한 방법으로 n=6 및 n=7에 대한 파스칼의 삼각형을 직접 만들어 보세요.

이제 파이썬 코드를 작성해 볼 차례입니다. 학습을 진행하면서 koreantech.org의 파이썬 IDE를 사용하여 코드를 직접 실행해 볼 수 있습니다.

파이썬 함수를 이용한 파스칼의 삼각형 출력

이제 주어진 행 수에 따라 파스칼의 삼각형을 출력하는 파이썬 함수를 만들어 보겠습니다. 여기서 고려해야 할 두 가지 중요한 사항이 있습니다.

파스칼의 삼각형의 각 숫자는 어떻게 표현할 수 있을까요?
적절한 간격과 형태로 파스칼의 삼각형을 어떻게 표시할 수 있을까요?

이제 이 질문에 대한 답을 찾아보겠습니다.

#1. 파스칼의 삼각형의 각 숫자를 계산하는 방법은 무엇일까요?

파스칼의 삼각형의 각 숫자는 조합 공식인 nCr을 사용하여 구할 수 있습니다. nCr은 n개의 항목 집합에서 r개의 항목을 선택하는 방법의 수를 나타냅니다.

nCr의 공식은 다음과 같습니다.

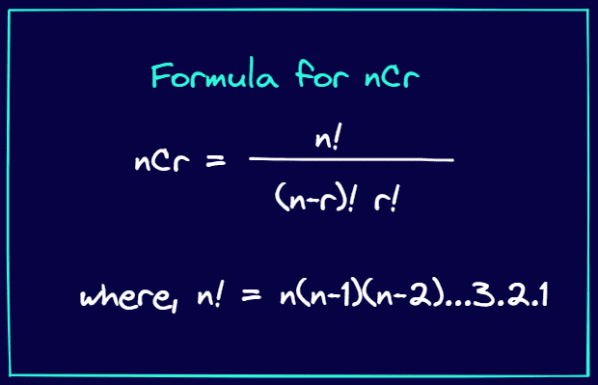
이 nCr 공식을 사용하여 파스칼의 삼각형의 항목을 표현하면 다음과 같습니다.

이제 각 숫자를 계산하는 방법을 알게 되었습니다.

#2. 삼각형 패턴을 유지하며 적절하게 간격을 맞추는 방법은 무엇일까요?

numRows 개의 행을 가진 파스칼의 삼각형에서 첫 번째 행은 하나의 숫자, 두 번째 행은 두 개의 숫자를 갖습니다. 파스칼의 삼각형 형태로 출력하기 위해, i번째 행에는 numRows – i 개의 공백이 앞에 필요합니다. 파이썬의 for 루프와 range 함수를 조합하여 이를 구현할 수 있습니다. range 함수는 기본적으로 끝점을 제외하므로, 필요한 선행 공백 수를 얻기 위해 +1을 추가해야 합니다.

각 숫자를 표현하는 방법과 삼각형을 출력할 때 공백을 처리하는 방법을 이해했으므로, 이제 pascal_tri 함수를 정의해 보겠습니다.

함수 정의 분석

pascal_tri 함수가 수행해야 할 작업은 다음과 같습니다.

pascal_tri 함수는 행의 수(numRows)를 인수로 받습니다.
numRows에 해당하는 파스칼의 삼각형을 출력합니다.

계승을 계산하기 위해 파이썬 내장 수학 모듈의 계승 함수를 사용합니다.

▶️ 다음 코드 블록을 실행하여 factorial 함수를 가져와 현재 모듈에서 사용해 보세요.

from math import factorial

아래 코드에는 함수 정의가 포함되어 있습니다.

def pascal_tri(numRows):
  '''numRows에 따른 파스칼 삼각형 출력'''
  for i in range(numRows):
      # 선행 공백을 위한 반복문
    for j in range(numRows-i):
          print(end=" ")
      # i번째 행의 숫자들을 출력하는 반복문
    for j in range(i+1):
          # nCr = n!/((n-r)!*r!)
          print(factorial(i)//(factorial(j)*factorial(i-j)), end=" ")
      # 각 행을 새로운 줄에 출력
    print("n")

이 함수의 작동 방식은 다음과 같습니다.

pascal_tri 함수는 하나의 필수 매개변수, 즉 행의 수(numRows)를 받습니다.
총 numRows개의 행이 있습니다. 각 행 i에 대해, 행의 첫 번째 숫자 앞에 numRows – i 개의 공백을 추가합니다.
그런 다음 nCr 공식을 사용하여 각 숫자를 계산합니다. i번째 행의 경우, 숫자는 j = {0, 1, 2, …, i}인 iCj입니다.
결괏값이 정수이기를 원하므로, 정수 나눗셈 연산자 //를 사용합니다.
각 행의 모든 숫자를 계산한 후, 새로운 줄에 다음 행을 출력합니다.

독스트링이 추가되었으므로, 파이썬의 내장 도움말 함수 또는 __doc__ 속성을 사용하여 함수의 독스트링에 접근할 수 있습니다. 아래 코드는 방법을 보여줍니다.

help(pascal_tri)

# 출력 결과
Help on function pascal_tri in module __main__:

pascal_tri(numRows)
    numRows에 따른 파스칼 삼각형 출력.

pascal_tri.__doc__

# 출력 결과
numRows에 따른 파스칼 삼각형 출력.

이제 행 수를 인수로 사용하여 함수를 호출해 보겠습니다.

pascal_tri(3)

# 출력 결과
     1
    1 1
   1 2 1

예상대로, 파스칼의 삼각형의 처음 3개 행이 출력됩니다.

재귀 호출을 이용한 파스칼의 삼각형 출력

이전 섹션에서는 파스칼의 삼각형의 각 숫자에 대한 수학적 표현을 확인했습니다. 하지만 인접한 두 행의 숫자들 사이의 관계를 활용하지 않았습니다. 사실, 이전 행을 사용하여 다음 행의 숫자를 계산했습니다. 이러한 관계를 사용하여 pascal_tri 함수의 재귀 호출을 구현할 수 있을까요?

물론입니다!

재귀 호출 함수에서는 기본 사례가 충족될 때까지 함수 스스로를 반복적으로 호출합니다. 파스칼의 삼각형을 구성할 때, 우리는 한 개의 숫자를 가진 첫 번째 행에서 시작하여 다음 행을 생성합니다.

따라서, pascal_tri(1)의 기본 사례에 도달할 때까지, pascal_tri(numRows)에 대한 함수 호출은 pascal_tri(numRows-1) 등을 순차적으로 호출합니다.

파스칼의 삼각형의 처음 세 행을 출력해야 하는 예를 들어보겠습니다. 다음 이미지는 재귀 호출이 스택에 어떻게 푸시되는지, 그리고 재귀 함수 호출이 파스칼의 삼각형 행을 어떻게 반환하는지를 보여줍니다.

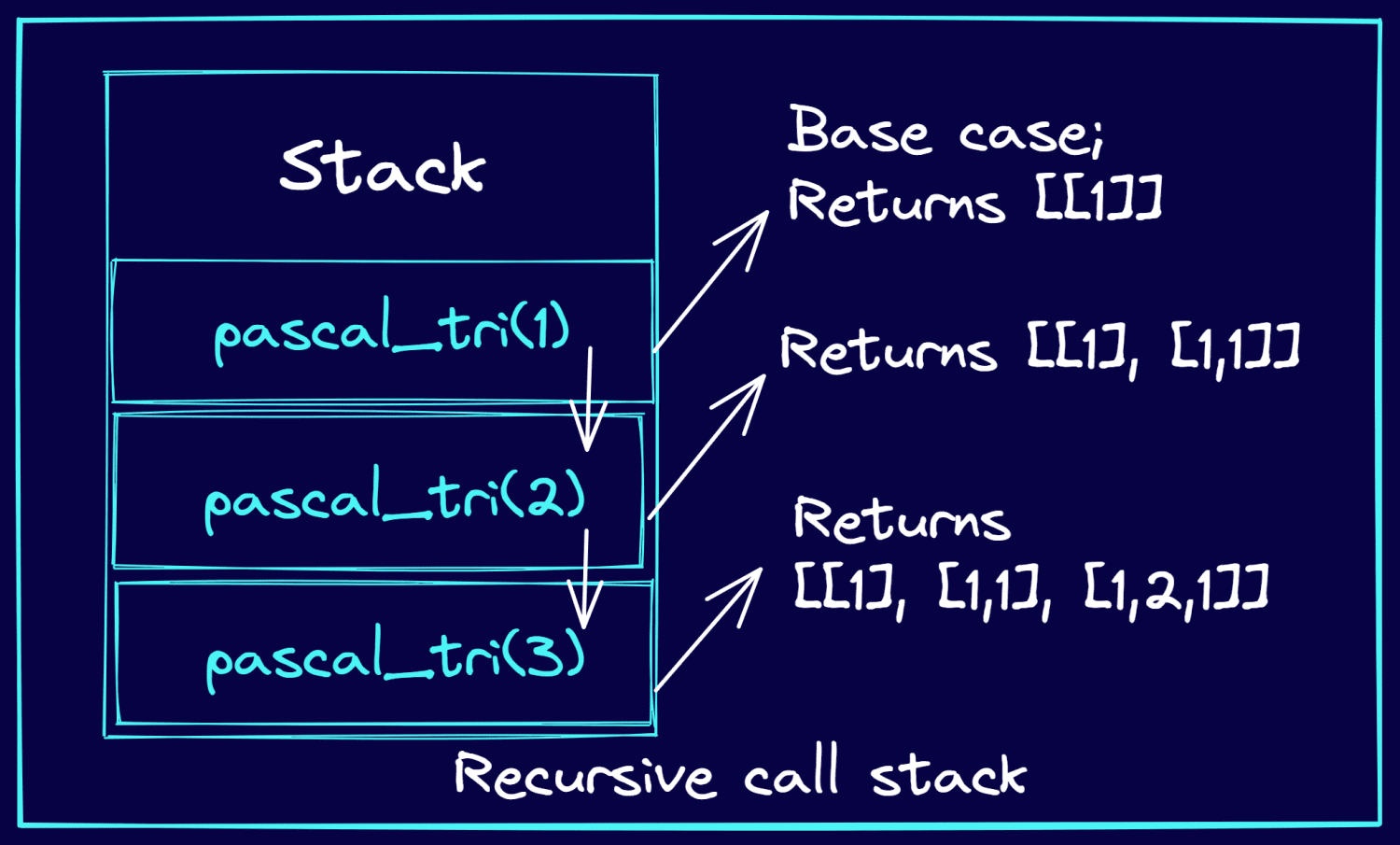
▶️ 아래 코드 블록을 실행하여 파스칼의 삼각형 행을 재귀적으로 생성해 보세요.

def pascal_tri(numRows):
    '''numRows에 따른 파스칼 삼각형 출력'''
    if numRows == 1:
        return [[1]]  # 기본 케이스
    else:
        res_arr = pascal_tri(numRows-1) # 재귀 호출
        # 이전 행을 사용하여 현재 행 계산
        cur_row = [1] # 모든 행은 1로 시작
        prev_row = res_arr[-1]
        for i in range(len(prev_row)-1):
            # 바로 위의 두 숫자의 합
            cur_row.append(prev_row[i] + prev_row[i+1])
        cur_row += [1]  # 모든 행은 1로 끝남
        res_arr.append(cur_row)
        return res_arr

여기서 주목해야 할 사항은 다음과 같습니다.

파스칼 삼각형의 각 행을 자체 목록으로 하는 중첩 목록 데이터 구조를 사용했습니다: [[row 1], [row 2], … ,[row n]].
pascal_tri(numRows) 함수 호출은 numRows – 1, numRows – 2, …, 1까지의 인수를 사용하여 재귀 호출을 트리거합니다. 이러한 호출은 스택에 푸시됩니다.
numRows == 1이면 기본 케이스에 도달하고, 함수는 [[1]]을 반환합니다.
이제 반환된 목록은 호출 스택의 후속 함수에서 다음 행을 계산하는 데 사용됩니다.
cur_row가 현재 행인 경우, cur_row[i] = 이전 행[i] + 이전 행[i+1]은 현재 인덱스 바로 위에 있는 두 숫자의 합입니다.

반환된 배열은 중첩 목록이므로, 아래 코드 블록과 같이 간격을 조정하고 숫자를 출력해야 합니다.

tri_array = pascal_tri(5)

for i, row in enumerate(tri_array):
  for j in range(len(tri_array) - i):
    print(end=" ") # 선행 공백
  for j in row:
    print(j, end=" ") # 숫자 출력
  print("n")  # 새 줄 출력

출력 결과는 다음과 같이 정확합니다!

numRows ≤ 5에 대한 파스칼의 삼각형을 출력하는 파이썬 함수

지금까지 배운 두 가지 방법 모두, 주어진 행 수에 상관없이 파스칼의 삼각형을 출력하는 데 사용할 수 있습니다. 하지만 적은 수의 행에 대해서만 파스칼의 삼각형을 출력해야 하는 경우가 있습니다. 출력해야 하는 행 수가 최대 5개인 경우, 간단한 방법이 있습니다.

아래 그림을 살펴보고, 11의 거듭제곱이 파스칼의 삼각형의 숫자와 어떻게 일치하는지 확인해 보세요. 이 방법은 11의 4제곱까지만 작동합니다. 즉, 11을 {0, 1, 2, 3, 4}의 거듭제곱으로 올리면 파스칼 삼각형의 1행부터 5행까지의 숫자가 됩니다.

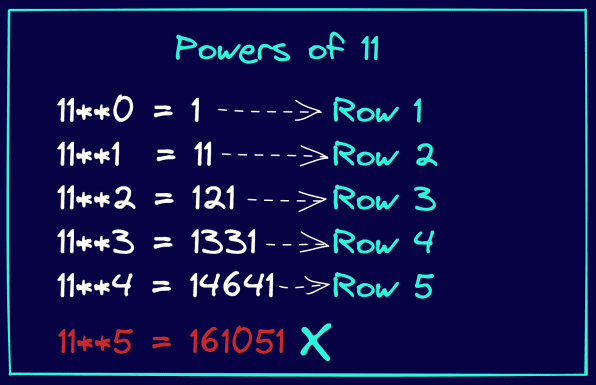
이제 함수 정의를 다음과 같이 다시 작성해 보겠습니다.

def pascal_tri(numRows):
  '''numRows에 따른 파스칼 삼각형 출력'''
  for i in range(numRows):
    print(' '*(numRows-i), end='')
    # 11의 거듭제곱 계산
    print(' '.join(str(11**i)))

pascal_tri 함수는 다음과 같이 작동합니다.

이전 예제와 같이 간격을 조정합니다.
그런 다음 파이썬의 지수 연산자 (**)를 사용하여 11의 거듭제곱을 계산합니다.
11의 거듭제곱은 기본적으로 정수이므로, str()을 사용하여 문자열로 변환합니다. 이제 문자열 형식의 11의 거듭제곱이 있습니다.
파이썬 문자열은 반복 가능하므로, 루프를 통해 문자 하나씩 접근할 수 있습니다.
다음으로, join() 메서드를 .join() 형식으로 사용할 수 있습니다. 여기서 는 구분 기호이고 의 요소들을 이 구분 기호를 사용하여 결합합니다.
여기에서는 문자 사이에 공백 하나가 필요하므로, 는 ‘ ‘이고, 은 문자열: 11의 거듭제곱입니다.

이제 함수가 의도한 대로 작동하는지 확인해 봅시다.

pascal_tri(5)

# 출력 결과
     1
    1 1
   1 2 1
  1 3 3 1
 1 4 6 4 1

다른 예로, 4를 인수로 하여 pascal_tri 함수를 호출해 보겠습니다.

pascal_tri(4)

# 출력 결과
     1
    1 1
   1 2 1
  1 3 3 1

1부터 5까지의 numRows에 대한 파스칼의 삼각형을 쉽게 출력하는 방법을 이해하셨기를 바랍니다.

결론

여기서 배운 내용은 다음과 같습니다.

주어진 행 수에 따라 파스칼의 삼각형을 구성하는 방법. 각 행의 모든 숫자는 바로 위의 두 숫자의 합입니다.
파스칼의 삼각형의 숫자를 계산하기 위해 nCr = n!/(n-r)!.r! 공식을 사용하여 파이썬 함수를 만드는 방법.
다음으로 함수의 재귀 호출 구현 방법을 배웠습니다.
마지막으로 11의 거듭제곱을 사용하여 최대 5개의 numRows에 대한 파스칼의 삼각형을 구성하는 가장 간단한 방법을 배웠습니다.

파이썬 기술을 향상시키려면 행렬을 곱하고 숫자가 소수인지 확인하고 문자열 조작 문제를 해결하는 방법을 배워보세요. 즐거운 코딩 되세요!