금융 세계에서 부채를 파악하는 것은 매우 중요한 일입니다. 사업을 운영하는 사업주, 학업에 열중하는 학생, 또는 단순하게 무언가를 구매하려는 개인 모두에게 대출금 계산 방법을 아는 것은 재정적 상황을 완전히 바꿀 수 있는 핵심 요소입니다.
마이크로소프트 엑셀은 이러한 작업을 훨씬 간편하게 만들어주는 강력한 도구인 PMT 함수를 제공합니다. 이 기능을 활용하면 대출에 대한 월별 상환액을 정확하게 산출하고, 정보에 근거한 현명한 재정 결정을 내릴 수 있게 됩니다.
엑셀 PMT 함수의 이해
매월 혹은 매년 납부해야 하는 대출금과 같이 복잡한 대출 상환 구조를 파악하는 것은 때로는 어렵게 느껴질 수 있습니다. 하지만 마이크로소프트 엑셀은 재무 분석을 위한 매우 효과적인 플랫폼이며, 그중 PMT 함수는 대출금 상환액 계산을 더욱 단순화해주는 유용한 도구입니다.
PMT 함수는 엑셀에서 제공하는 재무 함수 중 하나로, 대출이나 투자에 대한 정기적인 지불 금액을 계산하여 반환해줍니다. 이 함수는 지불액과 이자율이 기간 동안 일정하게 유지된다는 전제하에 작동합니다. 저축 계좌와 대출 모두에 적용될 수 있지만, 여기서는 대출에 초점을 맞추어 설명하겠습니다. PMT 함수의 기본 구조는 다음과 같습니다.
=PMT(이자율, 기간, 현재가치, [미래가치], [납입시점])
각 인수의 의미는 다음과 같습니다:
- 이자율(rate): 각 기간에 적용되는 대출 이자율입니다.
- 기간(nper): 총 지불 기간의 횟수입니다.
- 현재가치(pv): 대출 원금의 현재 가치입니다.
- 미래가치(fv): 선택적 인수로, 일반적으로 대출의 경우 생략하거나 0으로 설정합니다.
- 납입시점(type): 선택적 인수로, 지불 시점을 나타냅니다(0 = 기간 말, 1 = 기간 초).
PMT 함수는 이자율과 기간 값이 같은 시간 단위를 기준으로 입력되었을 때 정확한 결과를 산출합니다. 예를 들어, 기간 인수로 월별 납입 횟수를 입력했다면, 이자율 인수에도 월별 이자율을 입력해야 합니다.
대출 상황에서 현재가치는 대출 금액의 음수 값과 같습니다. 양수의 PMT 값은 0이 될 때까지 음수의 현재가치에 더해집니다. 대출금 상환이 목표이기 때문에, 미래가치는 기본적으로 0으로 설정됩니다. 납입시점 인수는 대부분의 은행이 기간 말에 지불을 처리하므로 생략하는 것이 일반적이며, 이는 디폴트 값으로 적용됩니다.
PMT 함수를 활용한 대출금 상환액 계산 방법
PMT 함수를 이용하면 대출을 포함한 모든 종류의 정기적인 지불에 대한 각 기간의 지불액을 산출할 수 있습니다. PMT 함수는 그 자체로 상환액을 계산해줄 뿐만 아니라, 몇 가지 간단한 공식 및 조정을 통해 다른 유용한 정보도 계산하는 데 도움을 줄 수 있습니다.
PMT 함수는 여러 인수를 사용하므로, 함수에 직접 값을 입력하는 것보다 각 인수를 별도의 셀에 입력하고, PMT 함수에서는 해당 셀을 참조하는 것이 효율적입니다.
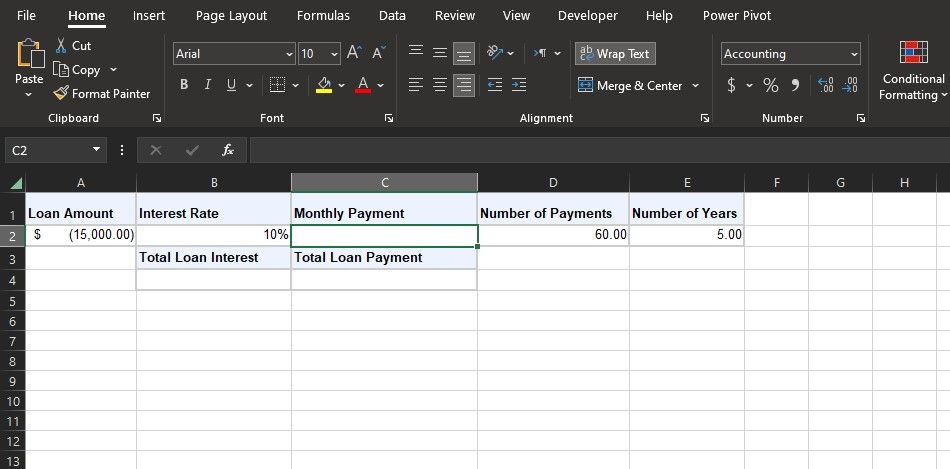
간단한 예시를 통해 알아보겠습니다. 5년 동안 연 10%의 이율로 15,000달러를 대출받는 상황을 가정해 봅시다. 이자와 상환금은 매달 말에 지불해야 하며, 매달 지불해야 할 금액을 알고 싶습니다.
가장 먼저 해야 할 일은 PMT 함수에 필요한 인수를 파악하는 것입니다. 이 예시에서 현재가치는 대출 금액의 음수 값인 -$15,000이고, 이자율은 월별 이자율(10%/12)이며, 총 지불 횟수는 60개월(5년)이 됩니다.
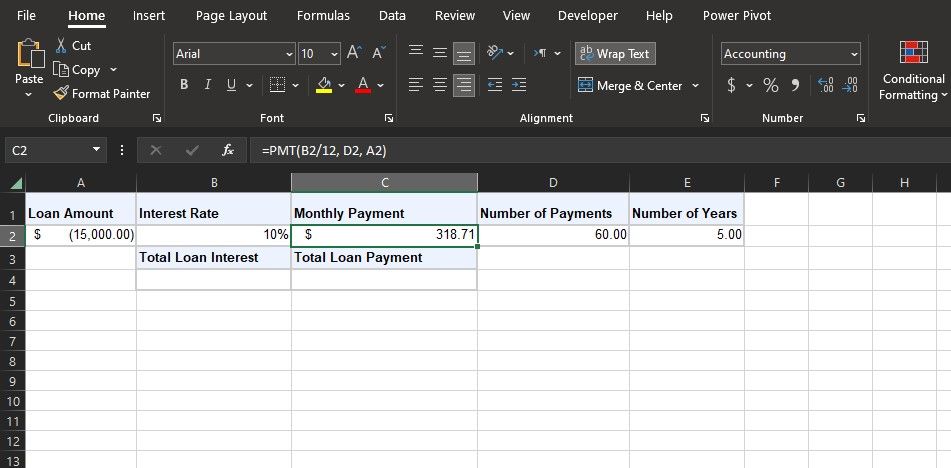
인수를 모두 파악했다면, PMT 함수를 사용해 대출 상환액을 빠르게 계산할 수 있습니다.
=PMT(B2/12, D2, A2)
이 공식에서 미래가치와 납입시점 인수를 생략하면 두 값 모두 0으로 설정되므로 문제없습니다. 다양한 값을 입력하며 상환액이 어떻게 변화하는지 확인할 수 있습니다.
총 대출금 상환액 계산
PMT 함수를 통해 얻을 수 있는 정보는 상환액만이 아닙니다. 간단한 공식을 활용하면 대출에 대한 더 명확한 그림을 얻을 수 있습니다. 다음 공식은 대출 기간 동안 총 지불해야 하는 금액을 계산합니다.
=C2*D2
이 공식은 PMT 값에 총 지불 횟수를 곱하는 것으로, 고정 상환액에 총 상환 횟수를 곱하여 전체 지불 금액을 산출합니다.

총 대출 이자 계산
또 다른 유용한 정보는 대출에 대한 총 이자입니다. 이를 통해 대출 원금 외에 은행에 지불해야 하는 이자 총액을 파악할 수 있습니다.
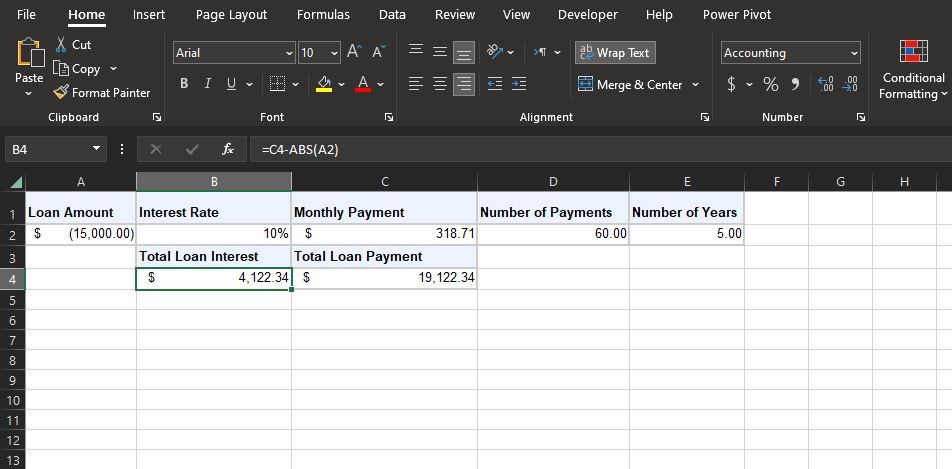
=C4-ABS(A2)
이 공식은 총 대출 상환액에서 대출 원금을 빼서 계산합니다. 대출 원금은 음수 값이므로, 수식에서는 ABS 함수를 사용하여 해당 셀의 절대값을 계산합니다.
엑셀 PMT 함수와 목표값 찾기 기능의 활용
지금까지 PMT 함수를 사용하여 대출에 대한 정기 상환액을 계산하는 방법을 알아보았습니다. 하지만 때로는 미리 특정 상환액을 설정해두고 싶을 수 있습니다. 예를 들어, 15,000달러 대출에 대해 월 500달러를 상환하는 것을 목표로 한다고 가정해 봅시다. 이럴 때 엑셀의 목표값 찾기 기능과 PMT 함수를 함께 활용하면 원하는 상환액을 만들어내는 인수 값을 찾을 수 있습니다.
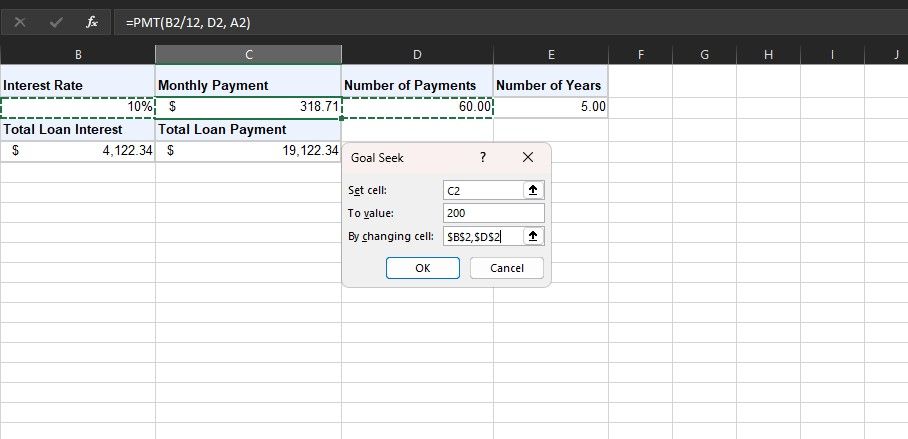
이 기능을 사용하면 목표 상환액을 달성할 때까지 다양한 인수 값을 자동으로 조정해볼 수 있습니다. 사용 방법은 다음과 같습니다:
이제 엑셀은 목표 상환액에 도달할 때까지 지정된 셀의 값을 자동으로 조정합니다. 목표값 찾기 기능을 활용하면 여러 개의 셀(예: 이자율과 대출 기간)을 동시에 변경하면서 목표 상환액을 달성할 수 있습니다.
이미 총 상환액과 총 이자를 계산했다면, 이 값을 목표값 찾기의 대상 셀로 설정할 수도 있습니다. 그러나 목표값 찾기 기능에 PMT 값을 직접 변경하도록 요청해서는 안 됩니다. PMT 함수를 덮어쓰게 되기 때문입니다. 이전과 마찬가지로, 대출 기간이나 이자율을 변경하며 원하는 결과를 얻을 수 있습니다.
이자율을 계산하고 싶다면 엑셀의 RATE 함수를 활용하면 빠르게 계산할 수 있습니다. RATE 함수는 고정 이자율을 반환합니다. 복리 계산이 필요한 경우에는 추가적인 계산기를 만들어야 할 수 있습니다.
엑셀 PMT 함수를 활용한 현명한 대출 관리
급변하는 현대 경제 환경에서, 자신의 재정적 의무를 정확히 이해하는 것은 매우 중요합니다. 엑셀의 PMT 함수를 사용하면 대출금 상환이라는 복잡한 과정을 효과적으로 관리할 수 있습니다.
주택 담보 대출, 자동차 대출, 혹은 다른 재정적 의무를 계획할 때, PMT 함수를 다른 엑셀 기능(예: 목표값 찾기)과 함께 활용하면 재무 결정에 대한 명확성과 확신을 얻을 수 있습니다. 엑셀의 강력한 기능을 활용하여 더욱 안정적인 재정적 미래를 만들어보세요.