소수 판별 파이썬 프로그램 작성 방법
이 튜토리얼에서는 주어진 숫자가 소수인지 여부를 판별하는 파이썬 프로그램을 만드는 방법을 상세히 설명합니다. 코딩 테스트를 준비하거나 수학 문제 해결을 위한 프로그래밍을 배우고 있다면, 소수 판별은 매우 유용한 기술입니다. 이 글을 통해 최적의 솔루션을 찾아가는 과정을 함께 살펴보겠습니다.
본 튜토리얼에서 다룰 내용은 다음과 같습니다:
- 소수의 기본 개념을 명확히 합니다.
- 주어진 숫자가 소수인지 확인하는 파이썬 코드를 작성합니다.
- 실행 시간 복잡도가 O(√n)인 효율적인 알고리즘을 구현합니다.
자, 이제 시작해 볼까요?
소수란 무엇인가?
가장 먼저 소수의 정의부터 살펴보겠습니다. 정수론에서, 자연수 n이 소수라는 것은 그 수가 정확히 두 개의 양의 약수를 갖는다는 의미입니다: 1과 자기 자신(n). 학교에서 배웠듯이, 어떤 숫자 i가 n을 정확하게 나눈다면 i는 n의 약수라고 합니다. ✅
다음 표는 몇 가지 숫자의 약수와 그 숫자가 소수인지 여부를 보여줍니다.
| n | 약수 | 소수 여부 |
| 1 | 1 | 아니오 |
| 2 | 1, 2 | 예 |
| 3 | 1, 3 | 예 |
| 4 | 1, 2, 4 | 아니오 |
| 7 | 1, 7 | 예 |
| 15 | 1, 3, 5, 15 | 아니오 |
위의 표에서 다음과 같은 사실을 알 수 있습니다:
- 2는 가장 작은 소수입니다.
- 1은 모든 숫자의 약수입니다.
- 모든 숫자 n은 자기 자신의 약수입니다.
따라서 1과 n은 모든 숫자 n의 자명한 약수입니다. 소수는 이 두 가지 외에 다른 약수를 가질 수 없습니다.
이것은 2부터 n-1까지의 숫자 중에서 n을 나누어떨어지게 하는 비자명한 약수를 찾을 수 없어야 함을 의미합니다.
파이썬에서 O(n) 시간 복잡도로 소수 판별하기
이제 위에서 설명한 접근 방식을 파이썬 함수로 구현해 보겠습니다.
파이썬의 range() 객체를 사용하여 2부터 n-1까지의 모든 숫자를 순회할 수 있습니다.
range(start, stop, step) 함수는 범위 객체를 반환합니다. 이 객체를 반복하면 start부터 stop-1까지 step 간격으로 숫자가 생성됩니다.
우리는 2부터 n-1까지의 정수가 필요하므로 range(2, n)을 지정하고 for 루프와 함께 사용할 수 있습니다.
구현할 내용은 다음과 같습니다:
- 만약 n을 나누어 떨어지게 하는 숫자를 찾으면, 즉시 n이 소수가 아니라는 결론을 내릴 수 있습니다.
- 만약 2부터 n-1까지의 모든 숫자를 순회하면서 n을 나누어 떨어지게 하는 숫자를 찾지 못했다면, n은 소수입니다.
소수 판별 파이썬 함수
위의 내용을 바탕으로 다음과 같이 is_prime() 함수를 정의할 수 있습니다:
def is_prime(n):
for i in range(2,n):
if (n%i) == 0:
return False
return True
이제 위 함수 정의를 분석해 보겠습니다.
- 함수 is_prime()은 양의 정수 n을 인수로 받습니다.
- (2, n-1) 범위에서 n을 나누어 떨어지게 하는 인수가 발견되면 함수는 숫자가 소수가 아니므로 False를 반환합니다.
- 만약 인수를 찾지 못하고 전체 루프를 완료하면 함수는 True를 반환합니다.
이제 몇 가지 인수를 사용하여 함수를 호출하고 결과를 확인해 보겠습니다.
is_prime(2)
# True
is_prime(8)
# False
is_prime(9)
# False
is_prime(11)
# True
위의 결과에서 2와 11이 소수임을 (함수가 True를 반환), 8과 9는 소수가 아님을 (함수가 False를 반환) 확인할 수 있습니다.
is_prime() 함수 최적화
여기서 약간의 최적화를 적용할 수 있습니다. 아래 표에 나열된 약수들을 살펴보세요.
| 숫자 | 약수 |
| 6 | 1, 2, 3, 6 |
| 10 | 1, 2, 5, 10 |
| 18 | 1, 2, 3, 6, 9, 18 |
n의 약수 중에서 n/2보다 큰 약수는 n 자신뿐임을 알 수 있습니다.
이는 n-1까지 반복할 필요가 없다는 것을 의미합니다. 대신, n/2까지만 루프를 실행하면 됩니다.
만약 n/2까지 비자명한 약수를 찾지 못했다면, n/2보다 큰 약수도 찾을 수 없습니다.
이제 is_prime() 함수를 수정하여 (2, n/2) 범위에서 약수를 검사하도록 하겠습니다.
def is_prime(n):
for i in range(2, int(n/2) + 1):
if (n%i) == 0:
return False
return True
몇 가지 함수 호출을 통해 결과를 확인해 보겠습니다.
is_prime(9)
# False
is_prime(11)
# True
최적화된 것 같지만, 이 알고리즘은 시간 복잡도 측면에서 이전 알고리즘과 동일하게 O(n)입니다. 즉, 실행 시간이 n 값에 비례하여 증가합니다.
더 나은 방법은 없을까요? 네, 있습니다!
▶️ 소수 판별의 시간 복잡도를 개선하는 방법은 다음 섹션에서 확인하세요.
파이썬에서 O(√n) 시간 복잡도로 소수 판별하기
숫자의 약수는 쌍으로 나타납니다.
만약 a가 숫자 n의 약수라면, axb = n을 만족하는 약수 b도 존재합니다. 즉, a * b = n 입니다.
예를 들어 확인해 보겠습니다.
아래 표는 쌍으로 나타나는 숫자 18의 약수들을 보여줍니다. 다른 숫자에 대해서도 같은 방식으로 확인할 수 있습니다.
참고로 √18은 약 4.24입니다.
(a, b) 쌍으로 나타나는 약수들 중 a가 4.24보다 작으면 b는 4.24보다 크다는 것을 알 수 있습니다. 예를 들어, (2, 9)와 (3, 6)입니다.
18의 약수 쌍
숫자 n이 완전제곱수라면, a = b = √n 이 약수 중 하나가 됩니다.
▶️ 아래 표에서 36의 약수를 확인해 보세요. 36은 완전제곱수이므로 a=b=6이 약수입니다. 다른 모든 약수 쌍(a, b)에 대해 a < 6 이면 b > 6 입니다.
36의 약수 쌍
정리하면 다음과 같습니다:
- 모든 숫자 n은 n = a * b 로 나타낼 수 있습니다.
- 만약 n이 완전제곱수라면 a = b = √n 입니다.
- 만약 a < b 라면, a < √n 이고 b > √n 입니다.
- 만약 a > b 라면, a > √n 이고 b < √n 입니다.
따라서 n/2까지 반복하는 대신 √n까지 반복하도록 선택할 수 있습니다. 이것은 이전 방식보다 훨씬 효율적입니다.
is_prime() 함수를 O(√n) 알고리즘으로 수정하는 방법
이제 파이썬에서 소수를 확인하는 함수를 최적화해 보겠습니다.
import math
def is_prime(n):
for i in range(2, int(math.sqrt(n)) + 1):
if (n%i) == 0:
return False
return True
위 함수 정의를 분석해 보겠습니다.
- 숫자의 제곱근을 계산하기 위해 파이썬의 내장 math 모듈을 가져와 math.sqrt() 함수를 사용합니다.
- n은 완전제곱수가 아닐 수 있으므로 정수로 변환해야 합니다. int(var)를 사용하여 var를 정수로 변환합니다.
- 실제로 √n까지 확인하고 있는지 확인하기 위해 range() 함수는 기본적으로 범위의 끝점을 제외하므로 1을 더합니다.
아래 코드 셀은 is_prime() 함수가 올바르게 작동하는지 확인합니다.
is_prime(8)
# False
is_prime(15)
# False
is_prime(23)
# True
다음 섹션에서는 O(n) 및 O(√n)을 시각적으로 이해하기 위해 몇 가지 간단한 그래프를 생성해 보겠습니다.
O(n)과 O(√n) 시각적으로 비교하기
▶️ 원하는 주피터 노트북 환경에서 다음 코드 스니펫을 실행하세요.
import numpy as np
import seaborn as sns
import pandas as pd
n = 20
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
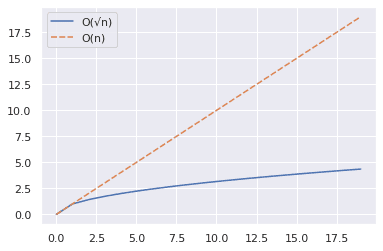
위 스니펫은 값의 범위에 대해 n과 √n 곡선을 그리는 방법을 보여줍니다.
- NumPy의 range() 함수를 사용하여 숫자 배열을 만듭니다.
- 그런 다음 n과 √n 값을 최대 20까지(미포함) 수집합니다. 데이터를 Pandas DataFrame에 저장합니다.
- 마지막으로 Seaborn의 lineplot() 함수를 사용하여 그래프를 생성합니다.
아래 그래프에서 √n이 n보다 훨씬 작음을 확인할 수 있습니다.

이제 범위를 최대 2000까지 늘리고 위와 동일한 단계를 반복해 보겠습니다.
import numpy as np
import seaborn as sns
import pandas as pd
n = 2000
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
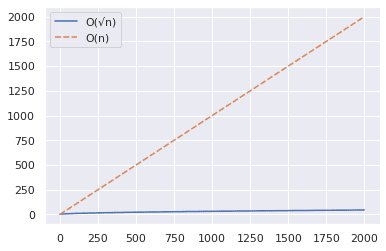
위 그래프에서 큰 숫자가 소수인지 테스트할 때 O(√n) 알고리즘이 훨씬 빠르다는 것을 알 수 있습니다.
간단한 예로 2377은 소수입니다. 직접 확인해 보세요! 😀
O(n) 접근 방식은 2000단계를 거쳐야 하지만, O(√n) 알고리즘은 단 49단계 만에 답에 도달할 수 있습니다.
결론
⏳ 이제 간단하게 요약할 시간입니다.
- 숫자가 소수인지 확인하는 가장 기본적인 방법은 (2, n-1) 범위의 모든 숫자를 반복하는 것입니다. 만약 n을 나누어 떨어지게 하는 약수를 찾지 못하면, n은 소수입니다.
- n/2보다 큰 n의 유일한 약수는 n 자신뿐이므로 최대 n/2까지만 검사하도록 선택할 수 있습니다.
- 위의 두 가지 방법 모두 시간 복잡도가 O(n)입니다.
- 숫자의 약수는 쌍으로 나타나므로 √n까지만 검사할 수 있습니다. 이 알고리즘은 O(n)보다 훨씬 빠르며, 특히 큰 수가 소수인지 여부를 확인할 때 더욱 효율적입니다.
파이썬에서 숫자가 소수인지 확인하는 방법을 이해하셨기를 바랍니다. 다음 단계로 문자열 연산에 대한 파이썬 튜토리얼을 확인해 볼 수 있습니다. 거기에서 문자열이 회문인지, 애너그램인지 등을 확인하는 방법을 배우게 될 것입니다.
다음 튜토리얼에서 다시 뵙겠습니다. 그때까지 즐거운 코딩하세요! 👩🏽💻